Większość wielkich matematyków odkryła ten temat w młodości i często przodują w międzynarodowych konkursach.
Natomiast matematyka była słabym punktem June Huh, która urodziła się w Kalifornii i wychowała w Korei Południowej. „Byłem dobry z większości przedmiotów z wyjątkiem matematyki” – powiedział. „Matematyka była średnio przeciętna, co oznacza, że na niektórych testach wypadłem całkiem dobrze, ale na innych prawie oblałem”.
Jako nastolatek dr Huh chciał zostać poetą i spędził dwa lata po ukończeniu szkoły średniej, goniąc za tym twórczym zajęciem. Ale żadne z jego pism nie zostało nigdy opublikowane. Kiedy studiował na Narodowym Uniwersytecie w Seulu, studiował fizykę i astronomię i rozważał karierę jako dziennikarz naukowy.
Patrząc wstecz, rozpoznaje przebłyski matematycznego wglądu. W gimnazjum w latach 90. grał w grę komputerową „The 11th Hour”. Gra zawierała łamigłówkę czterech rycerzy, dwóch czarnych i dwóch białych, umieszczonych na dziwnie małej szachownicy.
Zadanie polegało na wymianie pozycji czarno-białych rycerzy. Spędził ponad tydzień, przewracając się, zanim zdał sobie sprawę, że kluczem jest znalezienie pól, na które rycerze mogą się poruszać. Łamigłówkę szachową można przeformułować jako wykres, na którym każdy rycerz może przenieść się na sąsiednie wolne pole, a rozwiązanie można łatwiej zobaczyć.
Przeformułowanie problemów matematycznych poprzez ich uproszczenie i przetłumaczenie w sposób, który czyni rozwiązanie bardziej przejrzystym, było kluczem do wielu przełomowych odkryć. „Te dwie formuły są logicznie nie do odróżnienia, ale nasza intuicja działa tylko w jednej z nich” – powiedział dr Huh.
Zagadka matematycznego myślenia
Zagadka matematycznego myślenia
tutaj Puzzle pokonane w czerwcu huh:
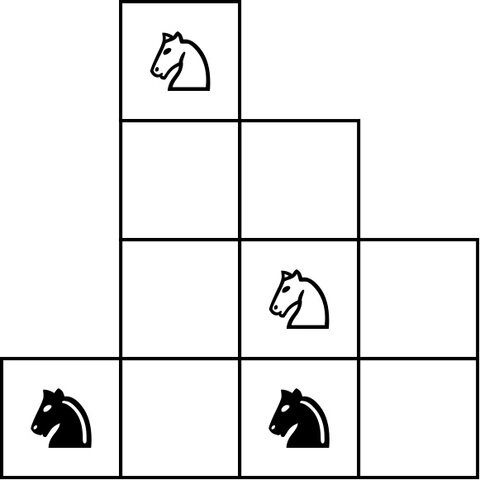
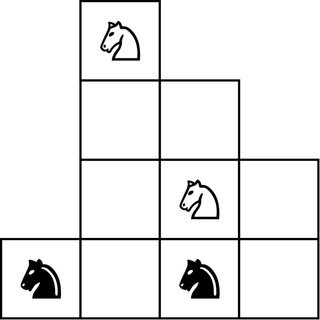
Bramka: Czarni i biali rycerze wymieniają się pozycjami. →
Matematykę odkrył ponownie dopiero na ostatnim roku studiów, kiedy miał 23 lata. W tym samym roku Hisuki Hironaka, japoński matematyk, który zdobył Medal Fieldsa w 1970 roku, był profesorem wizytującym na Uniwersytecie Narodowym w Seulu.
Dr Hironaka prowadził zajęcia z geometrii algebraicznej, na które uczęszczał dr Huh, na długo przed uzyskaniem doktoratu, myśląc, że mógłby napisać esej o doktorze Hironace. „Jest jak gwiazda w większości Azji Wschodniej” – powiedział dr Huh o dr Hironace.
Dr Huh powiedział, że kurs początkowo przyciągnął ponad 100 studentów. Jednak wkrótce większość uczniów uznała materiał za niezrozumiały i zrezygnowała z zajęć. Dr Huo kontynuował.
„Po jakichś trzech wykładach było nas jak pięciu” – powiedział.
Dr Huo zaczął jeść lunch z dr Hironaką, aby porozmawiać o matematyce.
„Głównie ze mną rozmawiał”, powiedział dr Huh, „a moim celem było udawanie, że coś rozumiem i odpowiadanie we właściwy sposób, aby rozmowa trwała dalej. To było trudne zadanie, ponieważ tak naprawdę nie wiedziałem o co chodzi.”
Dr Huh ukończył szkołę i rozpoczął pracę nad swoim tytułem magistra u dr Hironaki. W 2009 roku, kiedy dr Huh złożył podanie o doktorat do kilkunastu najlepszych szkół w Stanach Zjednoczonych.
„Byłem całkiem pewien, że pomimo wszystkich nieudanych zajęć z matematyki w moim transkrypcie na studiach licencjackich, otrzymałem entuzjastyczny list od medalisty Fieldsa, więc zostałbym przyjęty do wielu szkół podyplomowych”.
Wszyscy oprócz jednego go odrzucili — Uniwersytet Illinois Urbana-Champaign umieścił go na liście oczekujących, zanim ostatecznie go przyjął.
„To było bardzo interesujące kilka tygodni” – powiedział dr Huh.
W Illinois rozpoczął pracę, która doprowadziła go do przodu w dziedzinie kombinacji, dziedzinie matematyki, która określa liczbę sposobów mieszania rzeczy. Na pierwszy rzut oka wygląda to na zabawę z Tinker Toys.
Pomyśl o trójkącie, prostym obiekcie geometrycznym – który matematycy nazywają grafem – z trzema krawędziami i trzema wierzchołkami, w których spotykają się krawędzie.
Można wtedy zacząć zadawać pytania typu, przy danej liczbie kolorów, na ile sposobów można pokolorować wierzchołki, skoro żaden z nich nie może być tego samego koloru? Wyrażenie matematyczne, które daje odpowiedź, nazywa się wielomianem chromatycznym.
Bardziej złożone wielomiany chromatyczne można zapisać dla bardziej złożonych obiektów geometrycznych.
Używając narzędzi z jego pracy z dr Hironaką, dr Ho udowodnił przypuszczenie Reeda, który opisywał matematyczne właściwości tych modyfikatorów granic chromatycznych.
W 2015 roku dr Huh wraz z Ericiem Katzem z Ohio State University i Karimem Adepracito z Hebrajskiego Uniwersytetu w Jerozolimie zademonstrowali teorię Roty, która obejmowała bardziej abstrakcyjne obiekty kombinatoryczne znane jako matroidy niż trójkąty i inne wykresy.
W przypadku matroidów istnieje inna grupa wielomianów, które wykazują zachowanie podobne do wielomianów chromatycznych.
Ich dowód został wciągnięty do mistycznego kawałka geometrii algebraicznej znanego jako twierdzenie Hodge’a, nazwanego na cześć Williama Vallance Douglasa Hodge’a, brytyjskiego matematyka.
Ale to, co opracował Hodge, „było tylko jednym przykładem tej tajemniczej i uniwersalnej manifestacji tego samego wzorca we wszystkich dyscyplinach matematycznych” – powiedział dr Huh. „Prawda jest taka, że my, nawet najlepsi eksperci w tej dziedzinie, tak naprawdę nie wiemy, co to jest”.

„Avid bekonowy pionier. Niezależny rozwiązywacz problemów. Typowy myśliciel. Badacz podróży. Profesjonalny miłośnik zombie.